Coming under Coordinate Geometry, equations of straight lines appear across Cambridge IGCSE Mathematics Paper 2 and Paper 4. Below is a quick refresher on the theory plus guided examples so you can tackle any line question with confidence.

Parallel vs. Perpendicular Lines

Parallel lines

Parallel lines lie on the same plane, never meet, and always have identical gradients (slopes). If line 1 has a gradient of (+2), every line parallel to it will also have a gradient of (+2). The same applies to negative gradients: two lines with gradients (-5) are parallel.

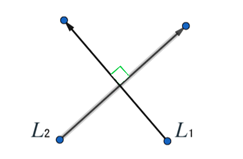
Perpendicular lines

Perpendicular lines meet at right angles. The gradients of two perpendicular lines multiply to give (-1):

[ \text{gradient}_1 \times \text{gradient}_2 = -1 ]

Exam-style example: proving lines are parallel

Points (A(-2,0)), (B(1,9)), (P(2,5)) and (Q(6,17)). Show that (AB \parallel PQ).

1. Find the gradient of (AB): [ m_{AB} = \frac{0-9}{-2-1} = \frac{-9}{-3} = +3 ]
2. Find the gradient of (PQ): [ m_{PQ} = \frac{17-5}{6-2} = \frac{12}{4} = +3 ]
3. Since the gradients are equal, (AB) is parallel to (PQ).

Exam-style example: proving lines are perpendicular

Points (A(-6,6)), (B(-8,-3)), and (C(1,-5)). Prove that (AB) is perpendicular to (BC).

1. Gradient of (AB): [ m_{AB} = \frac{-3-6}{-8+6} = \frac{-9}{-2} = \frac{9}{2} ]
2. Gradient of (BC): [ m_{BC} = \frac{-5+3}{1+8} = \frac{-2}{9} = -\frac{2}{9} ]
3. Product of gradients: [ \frac{9}{2} \times \left(-\frac{2}{9}\right) = -1 ] Therefore, (AB \perp BC).

The Equation of a Straight Line

Gradient (slope)

Use change in (y) over change in (x):

[ m = \frac{y_2 - y_1}{x_2 - x_1} ]

This holds for any non-vertical line.

Gradient–intercept form

Once you know the gradient (m) and the (y)-intercept (c) (where the line crosses the (y)-axis), you can write the line as:

[ y = mx + c ]

• If (c = 0), the line passes through the origin.
• If (m = 0), the line is horizontal.

General form

An alternative representation is:

[ ax + by + c = 0 ]

• If (a = 0) → line parallel to the (x)-axis.
• If (b = 0) → line parallel to the (y)-axis.
• If (c = 0) → line passes through the origin.

Equation-of-a-Line Problem Strategy

1. Identify what the question wants (parallel, perpendicular, specific coordinates, or intercepts).
2. Find gradients using coordinate pairs.
3. Substitute into (y = mx + c) (or the general form) to find the unknowns.
4. Check your answer against the context—does the line behave as expected?

Practice is everything. Attempt as many questions as you can, including the quiz below, to reinforce the process.

• IGCSE Equation of a Line quiz
• Join Tutopiya revision sessions

Watch: Equation of a Line Explained

About the author

Kulni Gamage is a contributing writer who breaks down tricky math concepts for IGCSE and GCSE learners. She focuses on practical strategies, engaging visuals, and resources that help students convert theory into exam-ready confidence.