- Coming under the topic of Coordinate Geometry, the equation of a line can be found in a variety of ways.
Watch the Video Below to Master the Equation of a Line ↓
Under the main topic of “Coordinate Geometry”, we will discuss in this article the subtopic of “Equation of a Line”.
To begin with, we will explore two key types of lines:
1. Parallel lines
2. perpendicular lines
1. Parallel lines
In geometry, parallel lines are two lines in the same plane that never meet and are equidistant from one another. Parallel lines can be extended infinitely, but regardless of how much these lines are extended, they will not meet each other, and therefore, will never intersect.
Parallel lines also have the same slope and are oriented at the same angle. This means that when we look at parallel lines on a calculation plane, these lines will have gradients that are exactly the same.
For example, if Line 1 at the top has a gradient of +2.
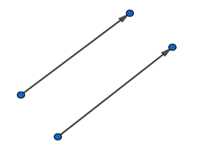
This can work the other way with negative gradients as well. If both lines are parallel, and there is a line with a gradient of -5, then the other line too will have the same gradient of -5. Hence even if the gradients of both these lines are negative, if they have the same value, we can come to the conclusion that these lines should be parallel to each other.
2. Perpendicular Lines
Perpendicular lines are those that are positioned at 90 degrees to each other. This means that we have a 90° (90-degree) angle between these lines.
The link that is to be found among the gradients of perpendicular lines is that if we multiply the gradients of the two perpendicular lines together, then it will always give us a value of -1. Therefore we say that the product of the gradients of two perpendicular lines would always give us -1 as an answer..
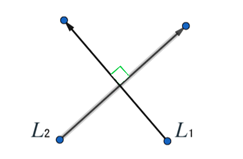
Parallel Lines and Perpendicular Lines in Exam Questions
So let’s go ahead and look at an example that shows us how we can deal with these parallel lines and perpendicular line facts in questions.
Example 1: The coordinates of four points A, B, P, and Q are (-2,0), (1,9), (2,5), and (6,17) respectively. Show that the line AB is parallel to the line PQ.
● The first step is to find out the gradient of the line AB.
In order to find out the gradient of the line, we need to find the change in y and divide it by the change in x. Or in other words, what we are going to do is take y2 – y1 and divide this by x2 – x1. In order to do that we consider what the relevant coordinates are.
We have (0 – 9) and we divide that by (-2 – 1). So (0 – 9) gives us -9 and (-2 – 1) gives us -3, and when we divide -9 by -3, we can get +3 as the answer. Therefore the radiant of line AB would be +3.
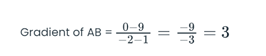
● Similarly we can do the same thing to work out the gradient of PQ. In this case it is going to be (17 – 5), divided by (6 – 2), which also gives us +3 as the answer.
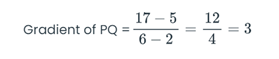
And now because the gradient of AB is the exact same as the gradient of PQ, we can come to the conclusion that our lines AB and PQ are parallel to each other.
Example 2: Prove that the lines AB and BC connected the points A (-6,6), B (-8, -3) and C (1,-5) are perpendicular to each other.
● To begin with, we must work out the gradient of AB.
To do this we will divide y2 – y1 by x2 – x1 like before, and this will result in the answer 9⁄2.
![]()
● We must then work out the gradient of line BC.
We follow the same step as above and this will give us the final answer of -2⁄9.
![]()
● To prove that these two lines are perpendicular to each other, we must work out the product of their gradients. If the final product of this multiplication results in -1, then we can prove that these two lines are perpendicular to each other.
When multiplying the two gradients 9⁄2 and -2⁄9 together, we will end up with -1 as the answer. This proves that these two lines AB and BC are perpendicular to each other, and thereby prove that these lines form a right angle between them.
![]()
The Equation of a Straight Line
When finding the equation of a straight line, one of the most important things to remember is to work out the gradient of the line.
To find out the gradient, we can once again rely on the change in y divided by the change in x.
The gradient of a line is usually denoted by the letter m.
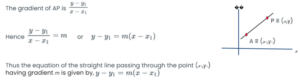
● In some questions we might be given the gradient, and if so, we can rearrange the equation and use it to find out an unknown coordinate if necessary.
● When we use this equation, another very important thing to remember is that we can also use this method to find the equations of straight lines that are not parallel to the y-axis (i.e. lines that are not vertical).
Gradient-Intercept Equation of a Straight Line
There are certain questions that are given at the exam where we are asked to find out what the y-intercept of a straight line is. This is usually denoted by the symbol c (a lowercase c).
The y-intercept is where the line intersects with the y axis. This would always have an x coordinate of zero (0) because this point would lie on the y axis and therefore it will always end up with an x coordinate of zero.
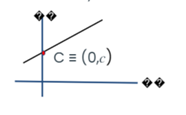
When we include the gradient and the intercept in the equation, we can form the general equation for any straight line. The general equation for any straight line is represented by y = mx + c, where m is the gradient and c is the y intercept.
The variables x and y can take many values and this would keep changing depending on the exact position that we look for in the straight line, but m would remain constant.
The General Equation of a Straight Line
We can also write the general equation of a straight line as ax + by + c = 0, and this is an alternative format of writing the equation.
![]()
In this format, if the value of a = 0, this would mean that the line is parallel to the x axis, and this would give us equations like y = 5, or y =-2. In these equations, we can see that we do not have an x term because our value of a is zero (zero multiplied by any value is zero itself).
On the other hand, if the value of b = 0 instead, this would give us lines that are parallel to the y axis, and this would give us equations like x = 5, x = 3. In these equations, we do not have a y term because our value of b is zero (zero multiplied by any value is zero itself).
If the value of c = 0, then this means that the straight line is passing through the origin of our coordinate axes and the origin is the coordinate (0,0), which is where your x axis and your y axis intercept each other.

This particular general equation can be used to derive all types of straight line graphs with the gradient of -a/b in the condition where b = 0.
Equation of a Line Questions
Check what the question asks of you and what answer you are supposed to provide. Based on the question, apply the relevant method and find the answer.
Practice as many questions as you can on this topic. You can find some questions in this quiz to check where you stand!
If you are struggling with IGCSE revision or the Mathematics subject in particular, you can reach out to us at Tutopiya to join revision sessions or find yourself the right tutor for you.
Watch the video below for a visual explanation to master the equation of a line!






