- A quadratic equation is a second-degree algebraic expression which can usually be seen in the form of ax2 + bx + c = 0, where a, b, and c are constants.
[Please watch the video attached at the end of this blog for a visual explanation on Mastering Quadratic Equations and Inequalities]
What is a quadratic inequality?
A quadratic inequality is an inequality where one variable is a value with a power of 2 (ex: x2).
If there is a power of 2, and that is the highest power that there is in your particular expression, it is considered to be a quadratic expression, and if it has any of these symbols: ≥, ≤, >, and <, then it becomes a quadratic inequality.
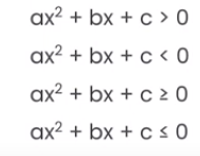
Quadratic equations
A quadratic equation is a second-degree algebraic expression which can usually be seen in the form of ax2 + bx + c = 0, where a, b, and c are constants.
There are a few methods we can use to solve quadratic equations. Something that must be remembered is that unlike linear equations, quadratic equations will give two different solutions.
This can mean that the same value appears twice for x, or that you get two values for x.
Method 1: Factorisation
This is done more or less using the method we studied under the Factorisation lesson. Refer to the example below to see how you would solve quadratic equations using factorisation.
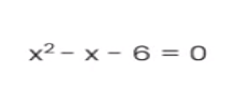
We have – 6 as the value of c, hence we need to consider the factors that can be multiplied together to give -6.
- – 3 * 2
- 2 * 3
- – 6 * 1
- -1 * 6
Once the factors are laid out as above, we need to see which factors add up to give -1 as that is the value we have in the middle (- x) where the constant b is – 1.
This leaves us the options of – 3 and + 2 as answers.
Hence the brackets can be written down as (x -3) and (x +2), and solving these two brackets gives us the answer that x is + 3 and x is -2.
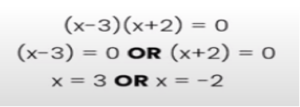
Sometimes, the equation is not given in the form of ax2 + bx + c = 0, in which case the equation must be rearranged so that all terms are brought to one side and the other side is equal to zero. Only then must the quadratic equation be solved.
There are also certain expressions where the middle term is absent (in the case the value of b = 0).
Factorisation can still be used in cases like this!
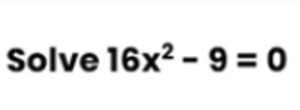
Both 16 and 9 in this case are square numbers, and we have a negative sign in the middle. This type of factorisation is known as “difference between the two squares”.
The square root of 16x2 is 4x, and the square root of 9 is 3. There has to be one positive bracket and another negative bracket (since the sign in between the two values is a negative sign). This will result in 4x + 3 and 4x – 3 as the two multiplications that are equivalent to zero.
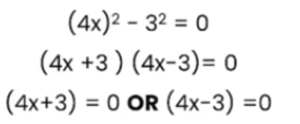
This can then be rearranged to find the value of x, and we can see that in this case the two values for x are x = +¾ and x = – ¾.

Method 2: Algebraic Manipulation
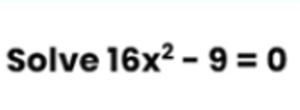
Another method which can be used to solve the above quadratic equation is via algebraic manipulation, which is where we rearrange and substitute for variables to obtain an algebraic expression in the form we need. We simply rearrange the formula given to us.
We must take – 9 over to the right hand side, so that the equation will read as 16x2 = 9.
Next, we divide 9 by 16 so that what remains on the left hand side is x2:
x2 = 9⁄16
In order to find the value of x, we need to find the square roots of both sides. The square root of x2 is x, and the square root of 9⁄16 is ¾. However, again, there is both a positive answer and a negative answer, as x = + ¾ and x = – ¾.
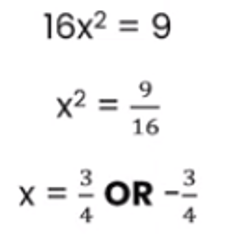
Method 3: Using a Formula
Whenever there is an equation that cannot be factorised or is very complicated, then the formula below can be used to solve the equation.

Ex:
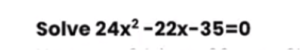
The first thing that must be done is the particular expression given in the question has to be rearranged so that it is in the ax2 + bx + c = 0 form. All the terms are on one side of the equation, and the other side must read as zero. (This is compulsory and extremely important)
We then look at the coefficients. In this case, the coefficients are:
a = + 24
b = – 22
c = – 35
Ensure that the sign in front of the coefficient is considered as well!
The next step is to carefully substitute the values into the formula and simplify the equation.
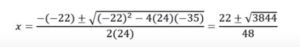
There are two solutions for x here, one negative and another positive.
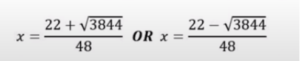
With the help of a calculator, the final answer can be figured out. It would be preferable if the answer could be rounded up to the 2nd decimal place or the to 3 significant figures (if it is not specified in the question).
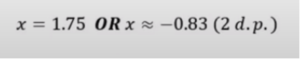
Mastering Quadratic Equations and Inequalities!
Quadratic Equations and Inequalities can be confusing to first time students. However, once you practise as many questions as possible, this will be quite simple. Some questions can be found here as well, and you can time your answers to see if you can stick to the time limit given.
Always remember that there are two values for x!
Make sure that you revise factorisation before attempting this lesson. You can find a video detailing factorisation here!
If you are struggling with IGCSE revision or the Mathematics subject in particular, you can reach out to us at Tutopiya to join revision sessions or find yourself the right tutor for you.
Watch the video below for a visual explanation of the lesson on mastering quadratic equations and inequalities. Don’t forget that there is a timed quiz to test whether you have understood the lesson!






