- Exponents are the index of a number and shows the number of times the multiplication is repeated. A surd is a radical which results in an irrational number.
[Please watch the video attached at the end of this blog for a visual explanation of exponents and surds, as well as how to use the calculator when solving such questions at the exam]
Square root this, square root that, cube root, radicals, and surds. All these terms might seem a bit odd to some people, but they should certainly not be odd concepts for a student sitting for Cambridge IGCSE Mathematics exams.
This blog article is focused on exponents and surds, a lesson that can seem confusing but is pretty easy once you get the hang of it!
Exponents/ Powers
To begin with, we will look at exponents, which can also be called powers or indices (singularly index). This shows us the number of times a number is multiplied by itself.
Ex: 2 ✖ 2 ✖ 2 ✖ 2 ✖ 2
If we look at the example given above, we can see that 2 is repeatedly multiplied by itself five times. This is difficult to write and is also time-consuming. Therefore instead of that, what you can simply do is write it as 25 (read as 2 to the power of 5). Once you see this expression, you will know that 2 is being multiplied by itself 5 times.
Or when you have to write an expression like this, you can see that the 2 is multiplied twice, so you write that as 22, 3 is multiplied twice so you write it as 32, and then there is the 5 at the end.
Or you have ⅓ being multiplied 4 times, which you can write as (⅓)4 (one-third to the power of four).
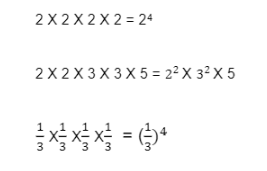
Rules regarding operations with powers
There are four rules regarding operations with powers.
Important:
In order for these rules to apply, the bases must be equal.
- When multiplying, the indices with equal bases, the powers are added.
Ex: 25 ✖ 23
Since both of them are based on two, the powers can be added (5 + 3), and this will add up to 2 to the power 8.
![]()
2. When dividing the indices with equal bases, the powers are subtracted.
Ex: 25 ÷ 23
Here, since both bases are 2, you can subtract the powers (5-3), which then gives you 2 to the power 2.
![]()
Remember:
- When multiplying, you have to add the powers, when dividing you have to subtract the powers,but this is only if the bases are equal.
3. Power of a power is obtained by multiplying the powers
Ex: (23)2
In order to find the answer to this example, you simply multiply the two powers together.(3 ✖ 2 = 6), therefore the answer is 2 to the power 6.
![]()
4. Negative power or an index can be converted into positive by taking the reciprocal.
Ex: 10-3
In order to make this a positive fraction, we need to make 10-3 the denominator. This will result in (1⁄103).
![]()
Similarly, when making a positive power a denominator, it will become a negative power.
Ex: 104 becomes (1⁄10-4 )
Refer to the video for calculator tips!
Roots
Roots are basically the inverses of powers. The root of a number is a number that when multiplied by itself gives the original number. They are usually denoted by the symbol √.
Ex:
PIC ∛, ∜, 5√
The above example will be read as 3 roots, 4 roots, and 5 roots.
If you have the square root of a number, you can convert that as a power of half.
Ex: √4
The square root of four can also be written as 4½. This can be simplified further.
4 = 2 ✖ 2, which, when written as a power of a number, is 22. Using the multiplication of powers rule, (2 ✖ ½ ) will give us 21 which is simply 2. Therefore, the square root of 4 is 2.
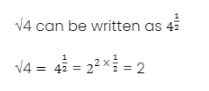
Ex: ∛27
The cubic root of 27 can also be denoted as 27⅓. This can be simplified further. 27 = 33, and using the power multiplication, (3 ✖ ⅓ ), this can be simplified into 31, which is simply 3. Hence, the cubic root of 27 is 3.
- If it is a square root, it is to the power of ½ (half), if it is a cube root, it is to the power of ⅓ (one-third).
Refer to the video for calculator tips here too!
Surds
A surd is a radical which will give us an irrational number as the answer (numbers that cannot be written as a fraction with both numerator and denominator being integers). A sure, therefore, is any number in which when you find the square root, instead of getting an integer value as an answer, all you get is a decimal answer.
Ex: ![]()
Therefore, the square root of a multiplied by the square root of b will be the same as finding the square root of a multiplied by b (ab). This is the first rule you must keep in mind.
Simplifying surds
Ex: √80
Since finding the square root of 80 straightaway would be a bit tricky, we can try simplifying it.If we consider 80 in multiples, 80 is the same as 16 ✖ 5.
This means, we can break √80 into √(16✖5), which further simplifies into √16 ✖ √5. AThe square root of 16 is 4 and we can then leave the answer as 4 √5.
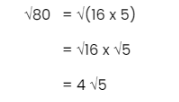
Sometimes we also get to simplify surds that look like the example below.
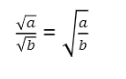
Ex: √27 ÷ √3
To simplify √27 ÷ √3, we can also write this as √(27/3). Once we divide 27 by 3, we get the answer to be 9. Hence, the square root of 9 is what we must find, resulting in 3 being the final answer.
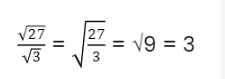
Rationalising Surds
In rationalizing surds, if we have a square root in the denominator, we try to get rid of it.
To do this, we multiply the top value and the bottom value by the same square root value.
Ex: In the example below, in order to get rid of √b, we must multiply both the denominator and numerator by √b.
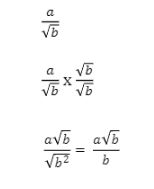
This will result in a√b being the numerator, and √b2 becoming the denominator.
The square root of b2 is going to be (2 ✖ ½) , therefore the denominator simplifies itself to be just b.
A numerical example can be seen below.
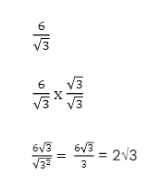
Adding and subtracting surds
Adding and subtracting surds is similar to adding and subtracting terms in algebraic expressions.
If you have two radicands (the number under the root symbol) that are the same, you can add them together.
If you are required to subtract radicands, then provided the radicand values are the same, then they can be subtracted.
However, if the radicands are different, then the surds cannot be added or subtracted.
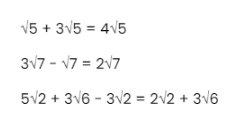
Helpful points for practicing exponents and surds for your upcoming Cambridge IGCSE Mathematics exams.
Mathematics is a subject that relies heavily on how well you prepare in advance for your exams. To make things easier, here are a few pointers that may help you get ready for your upcoming Cambridge IGCSE Mathematics exams.
Pay close attention to the powers and the roots. It is easy to get confused but this will result in you losing marks if you write the wrong answer. Take your time to attempt these questions, especially if they are long ones.
Practice sample questions – Practise, practice, practice. Questions on surds and exponents come in all shapes and sizes. They can sometimes be quite tricky, so do attempt all the questions you can get your hands on before exams. Our question banks have questions of different difficulty levels that you can practice before your actual exams.
Practice past paper questions to familiarise yourself with the format of the questions and paper.
Ask for help – You are never too late to ask for assistance if you’re struggling. Reach out to us at Tutopiya to find the right tutor to help you pass your exams with flying colors!
Watch the video below for a visual explanation of surds and exponents and attempt the quiz to challenge yourself!






