- Scalars are quantities with just a magnitude, whereas vectors are quantities that have both a magnitude and a size.
[Please watch the video attached at the end of this blog for a visual representation of Exploring Scalars and Vectors]
What are scalars?
Scalars are quantities that only consist of a magnitude/ size alone.
Ex: Mass, Length, Distance, Speed
What are vectors?
Vectors are quantities that consist of both a magnitude/size and a direction.
Ex: Weight, Displacement, Acceleration, Velocity
Measuring the resultant force of vectors
Most exam questions will ask students to find the resultant force where two forces are acting on a certain object.
We can do this using two methods:
1. The Triangle Method/ Head-to-Tail Method
2. The Parallelogram Method
1. The Triangle Method/ Head-to-Tail Method
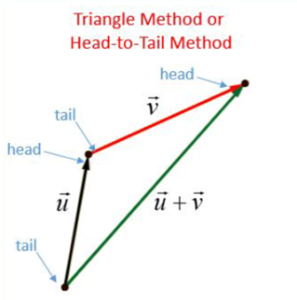
If this is the case, we need to draw these two arrows(as seen in the picture above) such that the head and the tail of both arrows are together. Therefore we place the vectors with the head of the first vector (u), connected to the tail of the next vector (v). We then connect the tail of the first vector to the head of the second vector, with the green arrow shown in the above diagram. That will be our resultant force and the direction of the arrow shows the direction of the resultant force.
If the original forces are in the clockwise direction, the resultant force will be in the anticlockwise direction and vice versa.
In order to find the magnitude of a resultant force in such a diagram where both u and v are given, we can draw the diagram to a scale (for example, 1N = 1 cm. Therefore if u = 5N, the line representing u will be 5 cm, and if v = 6N, then the line representing v will be 6 cm long). After drawing the diagram to a scale, we can then measure the length of the line joining the two forces to find the magnitude of the resultant force.
2. The Parallelogram Method
This method is quite similar to the triangle method, except with one key difference. Here. we have to place both vectors u and v at the same initial point (both vectors start from the same point) They start at the same point, but it must be drawn to scale and we have to be mindful of angles.
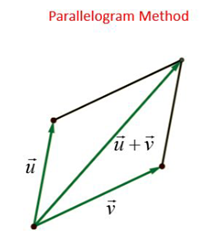
Once we do that, we must draw a parallelogram with these two lines. Once the parallelogram is formed, we have to draw the diagonal of the parallelogram starting from that same starting point, which will represent the resultant force. The arrowhead for that diagonal has to be away from the initial point, and if we measure the length of this resultant line, we will get the magnitude of the resultant force. Therefore, this parallelogram also needs to be drawn to a scale, much like the triangle method.
Finding the resultant of two perpendicular vectors acting on the same point
A very common scenario that we will come across in most exam questions, is to find the resultant of two perpendicular forces acting on the same point (one horizontal force and one vertical force exactly perpendicular to the other one).
In such a case, we can find the magnitude of the force by using the Pythagoras theorem and the direction of the vector quantity can be calculated using trigonometry.
- Using the Pythagorean theorem to find the magnitude of the vector
We use the head-to-tail method/ triangle method to draw a right angled triangle using the two forces given to us. We draw the horizontal force first and the vertical force next, where the head of the horizontal force meets the tail of the vertical force. Then we can complete the triangle.
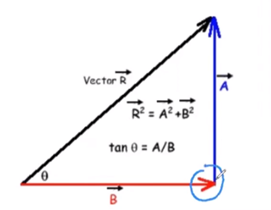
Because the vertical and horizontal forces are perpendicular, we will get a right angled triangle.
This method does not require us to draw the diagram to scale. The only thing that we must know is the magnitude of these forces. Using the Pythagorean theorem, if we square the sides that are on either side of the right angle and add them together, this will be equal to the square of the other side of the triangle (hypotenuse). Therefore even without drawing a scale diagram, we can simply use this formula to calculate the resultant force when we have two perpendicular forces. The only thing we need to do to find the magnitude of the resultant force would be to square the perpendicular forces, add them together, and find the square root of that answer.
In the example given below, both the original forces perpendicular to one another, are 11N each. Therefore we can square the first 11, add it to the square of the next 11, and then that whole answer needs to be squared to find the magnitude of R.
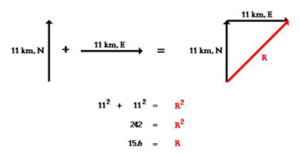
Once we do that we can find out that the magnitude of the resultant force R is 15.6 N.
Using Trigonometry to find the value of the angle, and thereby the direction of the resultant force
Now that we know the magnitude, we need to know how to find the value of the angle in order to know the exact direction of this resultant force.
In reality, we only need to know a few equations but to make life easier at the exam, it would be better to study all the derivations of the equations while studying this lesson.
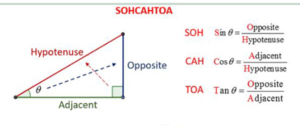
In trigonometry, we will learn the relationships of sides and angles when there is a right-angled triangle. If we consider the right-angled triangle found in the diagram below, ? (theta) is the angle that needs to be found out. The side that is opposite to ? is called the “opposite”. The longest side is always called the “hypotenuse”, and this is always the side that is in front of/ opposite to the right angle. The remaining side, which is exactly under ?, is called the “adjacent”.
Sin ? = Opposite/ Hypotenuse (SOH)
Cos ? = Adjacent/ Hypotenuse (CAH)
Tan ? = Opposite/ Adjacent (TOA)
These are the relationships we learn in Mathematics that we will use here to derive this equation.
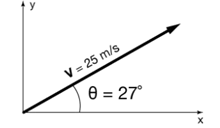
If we consider an example where the resultant v = 25m/s, and we are also given ? to be 27°, we are required to find vx and vy, the horizontal and vertical velocities respectively.
We can find out the value of vx (which is the adjacent side in this example) by using the equation CAH, where
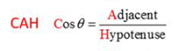
When we replace the values given to us, we can find out the value of vx.
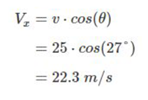
We can also find out the value vy using a similar method, but instead of using CAH equation, we will now use SOH, which is
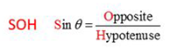
Once we replace the values here too, we will find out the value of vy.
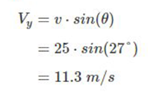
We can recheck whether the answers are correct. In order to do that, we can use the equation we have not used so far; TOA where
![]()
We can use this equation to find ? by also using the values we found for the velocities earlier.
Another mathematical relationship we learn of is that cos ? / sin ? = tan ? and that Tan ? = vx/ vy.
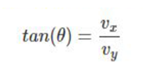
In a case where we know vx and vy, which is usually how the questions are, and we need to find ? in order to find the direction, all that must be done is apply this equation.
? = tan-1 (vx/vy).
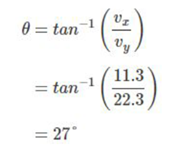
Calculator tip!
Press shift and click on “tan” in your calculator to get tan-1, or the tan inverse.
Watch the video on Exploring Scalars and Vectors to find out whether you are able to apply what you have learnt in a sample exam question!
Scalars and Vectors at Exams
Study the two equations discussed above, thoroughly. Also study the derivations of the equations since exam questions can come in a variety of ways.
Practise as many questions as you can on this topic. They are quite simple once you get the hang of them. You can find some questions in this quiz to check where you stand!
If you are struggling with IGCSE revision or the Mathematics subject in particular, you can reach out to us at Tutopiya to join revision sessions or find yourself the right tutor for you.






